一、随机变量
变量的值无法预先确定仅以一定的可能性(概率)取值的量。
强化学习中一般用大写的字母表示随机变量,用小写的字母表示随机变量的观测值(确定的值)。
比如:掷骰子中,用大写的变量 $X$ 表示可能掷出来骰子的值。假如掷一次骰子,得到它的值是2点,可以用小写的变量 $x$ 来表示,即 $x = 2$ 。
随机变量分两种基本的类型:离散型随机变量和连续型随机变量。
强化学习中训练不同类型的变量一般需要使用不同类型的算法,只有少部分算法同时支持两种类型的变量训练。
训练离散型随机变量使用的损失函数一般是交叉熵(Cross Entropy),而训练连续型随机变量使用的损失函数一般是均方误差(MSE, Mean Squared Error)。
二、概率密度函数(Probability Density Function,PDF)
描述随机变量的输出值,物理意义为随机变量在某个确定的取值点附近的可能性。
比如:掷骰子的概率密度函数 $p(X) = \frac{1}{6}$ 。
强化学习中的策略 $\pi$ 就是一个概率密度函数。因为它输出的其实是各个动作的概率。
因为概率的总和总是1,所以:
- 对于离散型随机变量 $X$ 及其可能值的集合 $\mathcal{X}$ 有:
- 对于连续型随机变量 $X$ 及其可能值的域 $\mathcal{X}$ 有:
三、期望
随机变量值产生的概率乘以随机变量值的总和。期望反应了随机变量平均取值的大小。
- 对于离散型随机变量 $X$ 及其可能值的集合 $\mathcal{X}$ ,其期望公式为:
- 对于连续型随机变量 $X$ 及其可能值的域 $\mathcal{X}$ ,其期望公式为:
四、强化学习模型
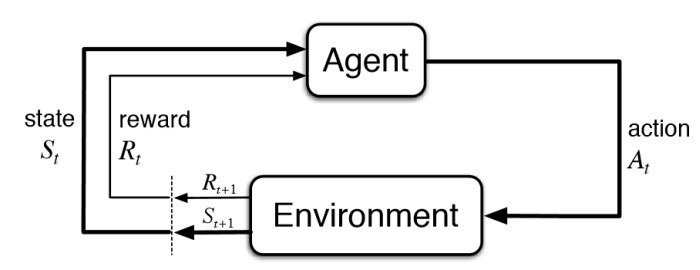
模型的构成:
智能体(Agent)
从环境中观测到状态(state)并执行某个动作(action)的对象。比如在马里奥游戏中,我们控制的马里奥角色就是智能体;在赛车游戏中,我们控制的赛车就是智能体。
与智能体紧密相关的概念是策略 $\pi$ 。 策略 $\pi$ 用来控制智能体,它的输入就是智能体观测到的状态,然后输出各个动作的概率。智能体执行的动作就是从这些动作概率中抽取出来的。策略 $\pi$ 其实就是一个概率密度函数,其数学定义为:
动作(Actios)
与环境交互时可以采取的动作的集合。比如在马里奥游戏中,可以采取的动作有:向左走、向右走、向上跳。
环境(Environment)
智能体所处的环境。比如在马里奥游戏中,就是指马里奥当前所处在的游戏环境。
状态(State)
智能体对环境的观测。比如在马里奥游戏中,游戏当前的画面就可以认为是环境当前的状态。
当智能体执行动作后,环境会进入到一个新的状态,这个就是状态转移的概念。状态转移的过程是随机的。这个随机性来自于两个方面:
- 智能体执行的动作是随机的。智能体由策略 $\pi$ 控制的,策略 $\pi$ 输出的是各个动作的概率。执行的动作是从这些动作概率中抽取出来的,所以说执行的动作是随机的。
环境本身的变化也是随机的。即使每次智能体执行的都是相同的动作,环境也会随机的变化。
比如在马里奥游戏中,即使每次都让马里奥向前走,但是游戏里的怪物总是会随机的移动,所以最后环境的状态也是随机的。
状态转移的随机性用数学表示为:
奖励(Reward)
智能体在环境中执行动作后获得的奖励或惩罚。比如在马里奥游戏中,吃到一个金币,就有金币奖励。
关于智能体对环境的观测的表述。用 state 时表示智能体能观察到环境的所有内部状态,用 observation 时表示智能体不能观察到环境的所有内部状态。比如玩围棋时用 state ,玩扑克牌时用 observation (因为你看不到别人手中的牌)。
交互的流程:
- 智能体从环境观测到状态 $s_t$ 。
- 智能体根据获取到的状态 $s_t$ 决定下一步采取动作 $a_t$ 。
- 环境执行动作 $a_t$ 后转移到新的状态 $s_{t+1}$ ,并给出智能体执行动作获得的奖励 $r_t$ 。
- 回到第1步。
第3步中获得的奖励 $r_t$ ,一些资料中也记为 $r_{t+1}$ 。比如:RL Course by David Silver - Lecture 2: Markov Decision Process 。
五、回报(Return)
强化学习的目的是让智能体与环境交互时获得的奖励尽可能的多。
智能体从 $t$ 时刻开始到游戏结束获得的所有奖励 回报(Return,Cumulative Future Reward) 为:
考虑到未来的奖励不如现在的奖励有价值,我们给未来的奖励加一个折扣系数 $\gamma$ ,且 $\gamma \in [0, 1]$ 。
所以智能体从 $t$ 时刻开始到游戏结束获得的所有奖励 折扣回报(Discounted Return,Cumulative Discounted Future Reward) 为:
根据马尔科夫回报过程我们可以知道,折扣回报也是一个随机变量,原因如下:
- 智能体采取的动作是一个随机变量:
- 环境状态的转移也是随机的:
而对于未来的任意时刻 $i \ge t$ ,奖励 $R_i$ 都依赖 $S_i$ 和 $A_i$ 。
比如在马里奥游戏中,如果马里奥头上有一个金币,这个时候向上跳就能获得金币奖励,但是如果这时不向上跳或者向上跳时头上没有金币都不能获得金币奖励。
所以,对某一个时刻 $t$ 的状态 $s_t$ 来说,折扣奖励 $G_t$ 依赖于未来所有的随机动作 $A_t, A_{t+1}, A_{t+2}, \cdots$ 和随机状态 $S_{t+1}, S_{t+2}, \cdots$ 。
折扣奖励 $G_t$ 定义了未来获取奖励的总和,机器学习的目的就是控制 agent 让 $G_t$ 的值越大越好。
六、动作价值函数(Action-Value Function)
由于 $G_t$ 是随机变量,在 $t$ 时刻并不能计算出 $G_t$ 的值。但是为了便于评估 $t$ 时刻的形势,消除 $G_t$ 中的随机性,可以对 $G_t$ 求期望,将随机性都用积分积掉,可以得到一个实数。即:
求期望得到的函数 $Q_{\pi}(s_t,a_t)$ 被称为动作价值函数。
把 $G_t$ 当做未来所有动作 $A$ 和所有状态 $S$ 的函数,除了 $a_t$ 和 $s_t$ ,其余的都用积分积掉。被积分积掉的变量包括 $A_{t+1}, A_{t+2}, \cdots$ 和 $S_{t+1}, S_{t+2}, \cdots$。
- 动作的概率密度函数为:
- 状态转移的概率密度函数为:
函数 $Q_{\pi}(s_t,a_t)$ 和当前的状态 $s_t$ 和动作 $a_t$ 有关。 $a_t$ 和 $s_t$ 当作被观测到的值来处理,而不是随机变量。函数 $Q_{\pi}(s_t,a_t)$ 还有策略 $\pi$ 有关,因为积分时会用到策略 $\pi$ 。
动作价值函数的意义在于可以评估策略 $\pi$ 在状态 $s_t$ 时采取动作 $a_t$ 的期望回报。即,策略 $\pi$ 处在状态 $s_t$ 时,动作价值函数 $Q_{\pi}(s_t,a_t)$ 可以给动作 $a_t$ 打分,用来判断执行动作 $a$ 是否明智。
就相当于你在打牌时有一个先知可以告诉你这次(仅一次)出每种牌后你赢钱的期望。
七、最优动作价值函数(Optimal Action-Value Function)
对函数 $Q_{\pi}(s_t,a_t)$ 做关于策略 $\pi$ 的最大化操作,就可以得到最优动作价值函数:
是 的简写。
最大化操作就是选取无数种策略中,让 $Q_{\pi}(s_t,a_t)$ 的值最大的那个策略 $\pi_*$ 。最优动作价值函数与策略 $\pi$ 无关,因为 $\pi$ 已经被最大化操作消除了。
最优动作价值函数的意义在于可以评估在状态 $s_t$ 时采取动作 $a_t$ 后最大能获得的期望回报。
就相当于在打牌时有一把牌让世界上牌技最好的人来玩时出每种牌后赢钱的期望。
八、状态价值函数(State-Value Function)
状态价值函数是动作价值函数关于动作的期望。
将动作 $A$ 视为随机变量,然后对动作价值函数 $Q_{\pi}(s_t,A)$ 关于动作 $A$ 求期望就可以得到状态价值函数:
状态价值函数 $V_{\pi}(s_t)$ 只与策略 $\pi$ 和状态 $s_t$ 有关。
状态价值函数可以反映策略 $\pi$ 处于状态 $s_t$ 时的优劣势。
比如下围棋时,状态价值函数可以反映出当前的局面是快赢了还是快输了等。
- 如果动作是离散型随机变量,则:
- 如果动作是连续型随机变量,则:
状态价值函数的意义在于可以评估策略 $\pi$ 处在状态 $s_t$ 时的期望回报。
就相当于你在打牌时,你拿了一把牌,有一个先知可以告诉你你玩这把牌赢钱的期望。
九、最优状态价值函数(Optimal State-Value Function)
对状态价值函数 $V_{\pi}(s_t)$ 做关于策略 $\pi$ 的最大化操作,就可以得到最优状态价值函数:
是 的简写。
最大化操作就是选取无数种策略中,让 $V_{\pi}(s_t)$ 的值最大的那个策略 $\pi_*$ 。最优状态价值函数与策略 $\pi$ 无关,因为 $\pi$ 已经被最大化操作消除了。
最优状态价值函数的意义在于可以评估在状态 $s_t$ 时最大能获得的期望回报。
就相当于在打牌时有一把牌让世界上牌技最好的人来玩时赢钱的期望。
十、用强化学习玩游戏
强化学习的目的就是学会如何控制智能体 ,让智能体基于当前的状态 $s$ 来做出相应的动作 $a$ ,争取能在未来获取尽量多的奖励。
强化学习通常要学习的是策略 $\pi(a|s)$ 或者最优动作价值函数 $Q_*(s, a)$,当有了这两个中的一个,就可以控制智能体自动的玩游戏了。
10.1 假如有一个好的策略
- 输入观测到的状态 $s_t$ 给策略 $\pi(a|s)$ ,它会返回不同动作的概率。
- 根据策略 $\pi(a|s)$ 返回的这些概率采样得到一个动作 $a_t$。
- 让环境执行动作 $a_t$ ,得到新的状态 $s_{t+1}$和奖励 $r_t$。
- 回到第1步。
好的策略相当于一个牌技好的人,牌技好的人赢钱的期望总是高。
所以我们直接训练出一个好的策略就可以了。
这种直接训练策略的方式就是强化学习中的 基于策略的学习(Policy Based Learning) 。
10.2 假如有最优动作价值函数
- 根据观测到的状态 $s_t$ 和最优动作价值函数 $Q_*(s_t,a_t)$ 计算出能够获得最大期望奖励的动作
- 让环境执行动作 $a_t$ ,得到新的状态 $s_{t+1}$ 和奖励 $r_t$。
- 回到第1步。
最优动作价值函数 $Q_*(s_t,a_t)$ 相当于一个先知,可以告诉我们出每种牌赢钱的期望,只要我们每次都出赢钱期望最大的牌,那么最后赢钱的期望就会最高。
所以我们也可以训练出一个先知,即最优动作价值函数。
这种训练最优动作价值函数的方式就是强化学习中的 基于价值的学习(Value Based Learning) 。
十一、熵
11.1 自信息
自信息(self-information) 表示一个随机事件所包含的信息量。
一个随机事件发生的概率越高,其自信息越低。如果一个事件必然发生,其自信息为 0。
对随机变量 $X$ ,其概率分布为 $P(x)$ ,当 $X = x$ 时,自信息 $I(x)$ 定义为:
11.2 信息熵
对于分布为 $P(x)$ 的随机变量 $X$ ,其熵(entropy)(自信息的期望)定义为:
信息论的基本定理之一指出,为了对从分布 $P$ 中随机抽取的数据进行编码,至少需要 $H[P]$ “纳特(nat)”对其进行编码。”纳特”相当于位,当时对数底为 $e$ 而不是 2,。因此,一个纳特是 $\frac{1}{log(2)} \approx 1.44$ 位。
信息熵表达随机变量所需的平均信息量。即 从不了解到了解一件事所需要的最小信息量。
11.3 交叉熵
对于分布为 $P(x)$ 的随机变量,熵 $H(P)$ 表示其最优编码长度。交叉熵是按照概率分布 $Q$ 的最优编码对真实分布 $P$ 的信息进行编码的长度(用 $Q$ 表示 $P$),定义如下:
交叉熵是一种分布描述另一种分布所需要的信息量。
11.4 KL 散度
KL 散度也叫 KL 距离 或者 相对熵,是用概率分布 $Q$ 来近似 $P$ 时所造成的信息损失量。
KL 散度是按照概率分布 $Q$ 的最优编码对真实分布 $P$ 的信息进行编码,其平均编码长度(交叉熵)$H(P,Q)$ 和 $P$ 的最优编码长度(熵) $H(P)$ 之间的差异。
对于离散概率分布 $P$ 和 $Q$ ,从 $Q$ 到 $P$ 的 KL 散度定义为:
KL 散度 总是非负的,即 $KL(P,Q) \ge 0$ ,可以衡量两个概率分布之间的距离。只有当 $Q = P$ 时, $KL(P,Q) = 0$ 。
十二、极大似然估计
极大似然估计,通俗理解来说,就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值。
十三、卷积神经网络
13.1 卷入神经网络的输出形状
若
- 输入形状为 $n_h \times n_w$
- 卷积核形状为 $k_h\times k_w$
- 上下各填充 $p_h$ 行,左右各填充 $p_w$ 列
- 垂直步幅 $s_h$ ,水平步幅 $s_w$
则输出形状为
十四、区分 Model-free 和 Model-based
What is the difference between model-based and model-free reinforcement learning?
区分某个强化学习算法是 model-based 还是 model-free 的:在 agent 执行它的动作之前,它是否能对下一步的状态和回报做出预测,如果可以,那么就是 model-based 方法,如果不能,即为 model-free 方法。
